• DENSITY
• DENSITY

• TOP
• PUBLICATIONS
• GROWTH MODE
• SHAPE
• DENSITY

Island density

Atoms diffuse randomly on a surface at a certain diffusion rate
and form islands when they meet each other.

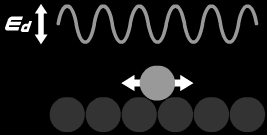
Fig. 1. Schematic illustration of diffusion barrier.

The diffusion rate can be given in the Arrhenius form by ν = ν₀exp(-E_d/k_BT),
where E_d is the diffusion barrier as shown in Fig. 1, ν₀ is the attempt frequency,
k_B is the Boltzmann factor, and T is the temperature.

The surface diffusion rate can be obtained by measuring the island density as a function of temperature.
Figure 2 shows STM images of Au islands grown on Ir(111) as a function of sample temperature.
The island density increases with decreasing sample temperature.

Fig. 2. STM images of Au islands grown on Ir(111) at (A) 300 K, (B) 160 K, and (C) 80 K.
Image sizes are (A) 1000×1000 nm², (B) 200×200 nm², and (C) 100×100 nm² (inset 15×15 nm²).

According to the mean-field nucleation theory [1], island density n is given by
n = η(4F/ν)^i/(i+2)exp(E_i/(i+2)k_BT),
where η is a numerical parameter, F is the deposition rate, i is the critical island size,
E_i is the binding energy of the i-island (E₁ = 0).
Figure 3 shows the Arrhenius plot of the Au island density on Ir(111).

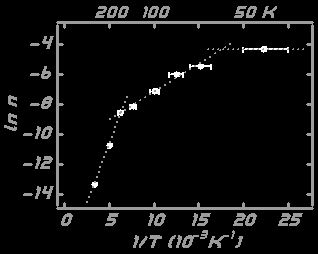
Fig. 3. Arrhenius plot of Au island density on Ir(111).

From the slope and intercept of the line in the Arrhenius plot in the range from 66 to 160 K (i = 1),
E_d = 0.094 ± 0.007 eV and ν₀ = 2.8×10^9±1.3 s^-1 have been estimated [2].