
Island shape
Au island shape depends on the underlying substrate [1].
Figure 1 shows STM images of Au islands grown on Ir(111) as a function of Au coverage.

Fig. 1. STM images of Au islands grown on Ir(111) at 300 K and Au coverages of (A) 0.52 ML, (B) 1.2 ML, and (C) 3.6 ML.
Image sizes are (A) 850×850 nm2, (B) and (C) 500×500 nm2.
The first-layer islands have a dendritic shape with a triangular envelope.
On the other hand, the second-layer islands have a triangularly compact shape,
and the third- or higher-layer islands have an irregularly compact shape.
In order to clarify the island growth mechanism,
a kinetic Monte Carlo (KMC) simulation program has been developed.
Terrace, corner, and edge diffusions shown in Fig. 2 are taken into account in the KMC simulation.
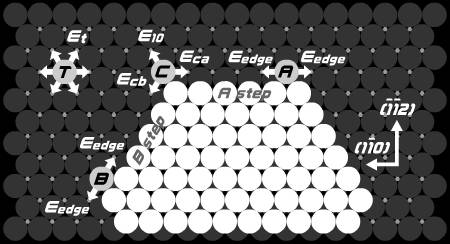
Fig. 2. Diffusion processes considered in the KMC simulation.
Et is the terrace diffusion barrier. Eca and Ecb are the corner diffusion barriers. Eedge is the edge diffusion barrier.
Figure 3 shows the simulation results at 300 K.

Fig. 3. Simulated islands as a function of Eedge under the condition of (A)-(E) anisotropic corner diffusion (Eca ≠ Ecb)
and (F)-(J) isotropic corner diffusion (Eca = Ecb).
Eedge is (A) 0.75, (B) 0.50, (C) 0.45, (D) 0.35, (E) 0.25, (F) 0.80, (G) 0.50, (H) 0.43, (I) 0.35, and (J) 0.25 eV.
Other parameters are Et = 0.094 eV and ν0 = 2.8×109 s-1, and F = 1×10-3 ML s-1.
The islands are dendritic when Eedge is higher, whereas they are compact when Eedge is smaller.
Furthermore, the islands have a triangular envelope when the corner diffusion is anisotropic (A - E),
whereas the island grow isotropically when the corner diffusion is isotropic (F - J).
These results show that the corner diffusion symmetry determines the island symmetry.
and that the edge diffusion determines the island compactness.
Figure 4 shows the fractal dimension of the islands obtained by the KMC simulations.

Fig. 4. Fractal dimension as a function of Eedge.
This continuous change of the fractal dimension has been explained
by relating the edge diffusion barrier with the growth probability at the island edge
by using the generalized diffusion limited aggregation model [2].
References
[1] S. Ogura et al., Phys. Rev. B 73, 125442 (2006).
[2] M. Matsushita et al., J. Phys. Soc. Jpn. 55, 2618 (1986).
