• GROWTH MODE
• GROWTH MODE

• TOP
• PUBLICATIONS
• GROWTH MODE
• SHAPE
• DENSITY

Growth mode

Atoms on an island feel an additional barrier to descend from the island as shown in Fig. 1.
This barrier is called Ehrlich-Schwoebel (ES) barrier.

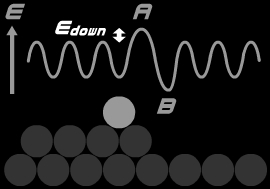
Fig. 1. Schematic illustration of the ES barrier.

The ES barrier determines the growth mode in the kinetic growth regime.
Figure 2 shows STM images of Au islands grown on Ir(111) at 100 K as a function of Au coverage [1].

Fig. 2. STM images (100×100 nm²) of Au islands grown on Ir(111) at 100 K and Au coverages of
(A) 0.32 ML, (B) 0.72 ML, (C) 1.2 ML, and (D) 2.3 ML.

The first Au layer grows in a layer-by-layer fashion (Fig. 2 A and B).
On the other hand, the second or higher Au layer grows in three-dimensional mode (Fig.2 C and D).

In order to derive the ES barrier, the KMC simulations were performed as a function of the ES barrier.
Figure 3 shows the simulation results at 100 K and a coverage of 0.72 ML.

Fig. 3. Simulation results as a function of Edown: (A) 0.02, (B) 0.04, and (C) 0.06 eV.
The lattice size is 400×460 and the coverage is 0.72 ML.

By comparing the fraction of the second-layer islands with experimental data,
the ES barrier has been estimated to be 0.035 eV on the first Au layer grown on Ir(111)
and 0.050 eV on the second Au layer grown on Ir(111).
This layer dependence of the step-down diffusion barrier can be explained
by the lattice mismatch between Au and substrate atoms.