
島の形状
Auの島の形状は下地に依存する.
図1はIr(111)上に300 Kで成長したAu島の蒸着量依存性を示したSTM像である[1].

図 1. Ir(111)上に成長したAu島の蒸着量依存性のSTM像.(A) 0.52 ML, (B) 1.2 ML, (C) 3.6 ML.
図のサイズ (A) 850×850 nm2, (B), (C) 500×500 nm2.
1層目は基板の3回対称性を反映した樹枝状島となることがわかった.
一方,2層目は3角形でコンパクトな形になり,3層目以降は不規則でコンパクトな島となった.
島の成長メカニズムを明らかにするために
図2に示すテラス,コーナー,エッジ拡散を取り入れたモンテカルロシミュレーションを開発した
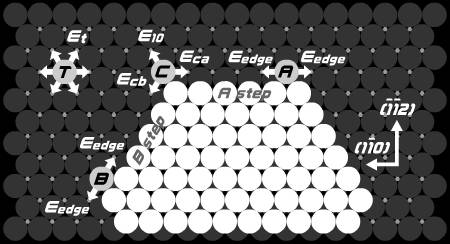
図 2.シミュレーションで考慮した拡散過程と拡散障壁.
Etはテラス拡散障壁,Eca,Ecbはコーナー拡散障壁,Eedgeはエッジ拡散障壁を示す.
図3に300 Kにおけるシミュレーションの結果を示す.

図 3. エッジ拡散障壁に対するシミュレーション結果.(A)-(E) Eca ≠ Ecb, (F)-(J) Eca = Ecb.
Eedge (A) 0.75, (B) 0.50, (C) 0.45, (D) 0.35, (E) 0.25, (F) 0.80, (G) 0.50, (H) 0.43, (I) 0.35, (J) 0.25 eV.
シミュレーションのパラメータ Et = 0.094 eV, ν0 = 2.8×109 s-1, F = 1×10-3 ML s-1.
島はエッジ拡散障壁が高いと樹枝状となり,低いとコンパクトになる.
さらにコーナー拡散が異方的(Eca ≠ Ecb)な場合,島は異方的となり基板の3回対称性を反映するが
コーナー拡散が等方的(Eca = Ecb)な場合,島は等方的に成長することがわかる.
これらの結果はコーナー拡散が島の対称性を決め,エッジ拡散が島のコンパクトさを決めることを示している.
図4はシミュレーションで得られた島のフラクタル次元を示している.

図 4. エッジ拡散障壁に対する島のフラクタル次元.
フラクタル次元がエッジ拡散障壁の関数として1.67から2へと連続的に変化することがわかった.
この連続的な変化は一般化拡散律速凝集モデル[2]を用いて
エッジ拡散係数と島の成長確率を結びつけることにより説明される.
References
[1] S. Ogura et al., Phys. Rev. B 73, 125442 (2006).
[2] M. Matsushita et al., J. Phys. Soc. Jpn. 55, 2618 (1986).
